競技プログラミングにハマって、そこで数論の知識とかあると有利になることがあるので数論を勉強し始めました
いざ勉強し始めてみるとプログラミングそっちのけで数論のほうが気になってしまい、ココ最近は仕事の後に数論の本を眺めていることが多いです
勉強するならブログにその成果というか、自分が考えたこととか書きたいなぁ、というかそのためにブログ作ったんじゃんと当初の目的を思い出しました
というわけで、今回はピタゴラス数の求め方について書いていきます
ピタゴラス数とは
ピタゴラス数の説明の前に、まずはピタゴラスの定理についてです
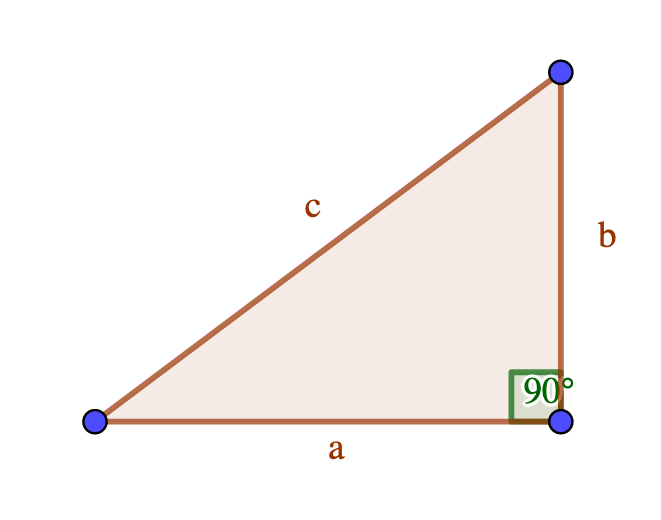
ピタゴラスの定理とは直角三角形において、その斜辺の長さの2乗は、そのほかの2つの辺それぞれの長さの2乗の和になるというやつです
式で書くと次のようになります
$$a^2+b^2=c^2$$
三平方の定理という名前でも知られていますね
このピタゴラスの定理を満たす3つの数字の組 \((a,b,c)\) をピタゴラス数と呼びます
ピタゴラス数は無限にある
よく知られたピタゴラス数として \((3,4,5)\) があります
\(\begin{aligned}3^2+4^2&=9+16\\&=25\\&=5^2\end{aligned}\)
実際に計算したところ成り立っていますね
つぎに、それぞれを2倍した \((6,8,10)\) について計算してみます
\(\begin{aligned}6^2+8^2&=36+64\\&=100\\&=10^2\end{aligned}\)
となり、成り立っています
\((a,b,c)\) をピタゴラス数、 \(k\) を整数として \((ka,kb,kc)\) がピタゴラス数になるか計算してみます
\(\begin{aligned}(ka)^2+(kb)^2&=k^2a^2+k^2b^2\\&=k^2(a^2+b^2)\end{aligned}\)
ここで、 \((a,b,c)\) はピタゴラス数ですから、
\(a^2+b^2=c^2\)
が成り立ちます
よって、
\(\begin{aligned}(ka)^2+(kb)^2&=k^2(a^2+b^2)\\&=k^2c^2\\&=(kc)^2\end{aligned}\)
となり、 \((ka,kb,kc)\) はピタゴラス数となります
この結果から何かしらピタゴラス数を一組みつけたら、その整数倍もピタゴラス数になるため無限にピタゴラス数を見つけることができます
 hansode
hansode原始ピタゴラス数
\((3,4,5)\) の整数倍の組が全部ピタゴラス数になるからと言って、ピタゴラス数を全部見つけたとは思えません
実際、ピタゴラス数には \((3,4,5)\) 以外に、 \((5,12,13)\) や \((7,24,25)\) があります
あるピタゴラス数の定数倍のピタゴラス数をみつけてもあんまり嬉しくないので、定数倍じゃないピタゴラス数を見つけようと思います
つまり、共通の因数を持たないピタゴラス数を求めていきます
ちなみに、共通の因数を持たないピタゴラス数を原始ピタゴラス数といいます
中学生の時に思いついた方法
ちょっと余談ですが、ピタゴラスの定理は中学生の時に習うと思います
中学生だった当時、因数分解とピタゴラスの定理の両方を習ったので、
\(a^2+b^2=c^2\)
という式をみたら、
\(\begin{aligned}a^2&=c^2-b^2\\&=(c+b)(c-b)\end{aligned}\)
と因数分解したくなりました
この式変形を利用してピタゴラスの定理を満たす整数をみつけられないかなと考えたことがあります
 hansode
hansodeとなると、 \(c=b+1\) となり \(c,b\) は共通の因数を持たなさそうです。コレを元の式に代入して、
\(a^2=2b+1\)
となります
右辺は \(3\) 以上の奇数ならなんでもOKとなるので、 \(a\) に奇数を代入すれば \(a^2\) は奇数となり、それをみたす \(b\) も見つかります
\(a=3\) を代入すると \(3^2=9=2\times 4+1\) となり、 \(b=4,c=5\) が求まり、ピタゴラス数 \((3,4,5)\) が見つかります
\(a=5\) を代入すると \(5^2=25=2\times 12+1\) となり、 \(b=12,c=13\) が求まり、ピタゴラス数 \((5,12,13)\) が見つかります
ココまではいい感じだったんですが、 \(c-b=2,3,4\dots\) のときについても調べないといけないんだろうなと思って、そこで考えるのをやめました
というわけで、この話題は中学生の時に抱いた疑問を解決してくれると思ったので、勉強にも力が入りました笑
原始ピタゴラス数の求め方
数の偶奇から条件を求めてみる
それでは原始ピタゴラス数を求めていこうと思います
まず、原始ピタゴラス数 \((a,b,c)\) の組は偶数、奇数どのような組み合わせを取りうるか調べます
愚直に数え上げてみると、次の8通りが考えられます
(偶,偶,偶)
(偶,偶,奇)
(偶,奇,偶)
(偶,奇,奇)
(奇,偶,偶)
(奇,偶,奇)
(奇,奇,偶)
(奇,奇,奇)
\((a,b,c)\) が、(偶,偶,奇),(偶,奇,偶),(奇,偶,偶),(奇,奇,奇)のときは両辺の偶奇が一致しないため等式が成り立ちません
(偶,偶,偶)(偶,偶,奇)(偶,奇,偶)
(偶,奇,奇)(奇,偶,偶)
(奇,偶,奇)
(奇,奇,偶)(奇,奇,奇)
\((a,b,c)\) が(偶,偶,偶)のときは2を共通因数に持つため除外する
\((a,b,c)\) が(奇,奇,偶)のときは、 \(a=2l+1,b=2m+1,c=2n\) として計算してみると、
\(\begin{aligned}a^2+b^2&=(2l+1)^2+(2m+1)^2\\&=(4l^2+4l+1)+(4m^2+4m+1)\\&=4(l^2+l+m^2+m)+2\end{aligned}\)
\(\begin{aligned}c^2&=(2n)^2\\&=4n^2\end{aligned}\)
\(a^2+b^2\) も \(c^2\) も偶数になっていますが、 \(c^2\) は \(4\) で割れて \(a^2+b^2\) は \(4\) で割れません
等式が成り立っていません
よって(奇,奇,偶)の組の数がピタゴラスの定理を満たすことはありません
(偶,偶,偶)(偶,偶,奇)(偶,奇,偶)
(偶,奇,奇)(奇,偶,偶)
(奇,偶,奇)(奇,奇,偶)(奇,奇,奇)
愚直に数え上げてみた8通りのうち残ったのは、
(偶,奇,奇)
(奇,偶,奇)
となります。
ピタゴラスの定理について \(a\) と \(b\) を入れ替えてもそんな問題なさそうなので、 \(a\) は奇数で \(b\) は偶数で考えていこうと思います
現時点で原始ピタゴラス数 \((a,b,c)\) があるなら、 \(a,b,c\) には共通の因数がなくて、 \(a\) は奇数、 \(b\) は偶数、 \(c\) は奇数という条件になりそうです
共通因数がないことから条件を求めてみる
原始ピタゴラス数 \(a,b,c\) の偶奇についてハッキリしたと思いますが、この条件だけでは原始ピタゴラス数を全部見つけるのは難しそうです
つぎに、 \(a,b,c\) に共通因数がないことからなにか条件を求められないか考えてみます
まず、ピタゴラスの定理で移項して因数分解してみます
\(\begin{aligned}a^2+b^2&=c^2\\a^2&=c^2-b^2\\&=(c+b)(c-b)\end{aligned}\)
ここで、 \((c+b)\) と \((c-b)\) に注目します
\(c\) と \(b\) に共通因数がなければ、 \((c+b)\) と \((c-b)\) にも共通因数がなさそうな気がします
\((c+b)\) と \((c-b)\) に共通因数があると \(a,b,c\) が共通因数を持ってしまい、原始ピタゴラス数の定義と矛盾することを示そうと思います
仮に \((c+b)\) と \((c-b)\) に共通因数 \(d\) があるとすると、 \(c+b=k_{1}\times d, c-b=k_{2}\times d\) と表せます
\((c+b)+(c-b)=2c\) 、 \((c+b)-(c-b)=2b\) であることから、
\(\begin{aligned}(c+b)+(c-b)&=k_{1}d+k_{2}d\\&=d(k_{1}+k_{2})\\&=2c\end{aligned}\)
\(c=\dfrac{d(k_{1}+k_{2})}{2}\)
\(\begin{aligned}(c+b)-(c-b)&=k_{1}d-k_{2}d\\&=d(k_{1}-k_{2})\\&=2b\end{aligned}\)
\(b=\dfrac{d(k_{1}-k_{2})}{2}\)
となり、 \(b,c\) は共通因数 \(d\) を持つことになります
また、
\(\begin{aligned}a^2&=(c+b)(c-b)\\&=k_{1}d\times k_{2}d\\&=k_{1}k_{2}d^2\end{aligned}\)
\(a=d\sqrt{k_{1}k_{2}}\)
となるため、 \(a\) も因数に \(d\) を持ってしまいます
\(a,b,c\) は共通因数 \(d\) を持つため原始ピタゴラス数であることに矛盾します
\((c+b)\) と \((c-b)\) に共通因数があると仮定したことによって矛盾が導かれたので、 \((c+b)\) と \((c-b)\) に共通因数はありません
それでは \((c+b)\) と \((c-b)\) に共通因数がないとどんなことがいえるでしょうか
\(a^2=(c+b)(c-b)\)
というのは何回も登場していますが、左辺の \(a^2\) は明らかに平方数です
そしたら右辺も平方数になりますが、 \((c+b)\) と \((c-b)\) に共通因数がないことから \((c+b)\) と \((c-b)\) がそれぞれ平方数になります
 hansode
hansode\(b\) は偶数、 \(c\) は奇数としたので、 \(s,t(s>t)\) を共通因数を持たない奇数として、
\(\begin{aligned}c+b&=s^2\\c-b&=t^2\end{aligned}\)
と表すことができます
それではコレまで登場した式を整理していきます
\(\begin{aligned}2c&=(c+b)+(c-b)\\&=s^2+t^2\\c&=\dfrac{s^2+t^2}{2}\end{aligned}\)
\(\begin{aligned}2b&=(c+b)-(c-b)\\&=s^2-t^2\\b&=\dfrac{s^2-t^2}{2}\end{aligned}\)
\(\begin{aligned}a^2&=(c+b)(c-b)\\&=s^2t^2\\a&=st\end{aligned}\)
となります
結果
コレまでの結果を踏まえて、原始ピタゴラス数 \((a,b,c)\) は共通因数を持たない奇数 \(s,t(s>t)\) を用いて、
\((st,\dfrac{s^2-t^2}{2},\dfrac{s^2+t^2}{2})\)
と表すことができます
 hansode
hansode試しに求めてみる
それでは求めた結果を用いて好きなだけピタゴラス数を求めてみようと思います
手でやるのはツライのでコンピュータに計算させてみます
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int a,b,c;
for (int i = 3; i < 16; i += 2)
{
for (int j = 1; j < i; j += 2)
{
if(gcd(i, j) != 1) continue;
a = i*j;
b = (i*i - j*j)/2;
c = (i*i + j*j)/2;
if(a*a + b*b == c*c)
{
cout << "ok: (a,b,c) = (" << a << ", " << b << ", " << c << ")" << endl;
}
else
{
cout << "ng: (a,b,c) = (" << a << ", " << b << ", " << c << ")" << endl;
}
}
}
return 0;
}競プロの環境をそのまま使っているので、includeのところが一般的じゃないかも知れませんが、ご容赦ください…
\(i,j\) に共通因数なし(互いに素)であることを確認するため、gcd(i,j)で最大公約数が \(1\) であることを確認しています
(もし共通因数があるなら \(1\) より大きいので、その数になりますね)
基本的にこのコードで作る数の組はピタゴラスの定理を満たすと思いますが、もし満たさないことがあったら困るので、失敗する場合も表示させます
\(i\) が \(15\) までの範囲で原始ピタゴラス数を求めていきます
実行してみた結果は以下のようになります
ok: (a,b,c) = (3, 4, 5)
ok: (a,b,c) = (5, 12, 13)
ok: (a,b,c) = (15, 8, 17)
ok: (a,b,c) = (7, 24, 25)
ok: (a,b,c) = (21, 20, 29)
ok: (a,b,c) = (35, 12, 37)
ok: (a,b,c) = (9, 40, 41)
ok: (a,b,c) = (45, 28, 53)
ok: (a,b,c) = (63, 16, 65)
ok: (a,b,c) = (11, 60, 61)
ok: (a,b,c) = (33, 56, 65)
ok: (a,b,c) = (55, 48, 73)
ok: (a,b,c) = (77, 36, 85)
ok: (a,b,c) = (99, 20, 101)
ok: (a,b,c) = (13, 84, 85)
ok: (a,b,c) = (39, 80, 89)
ok: (a,b,c) = (65, 72, 97)
ok: (a,b,c) = (91, 60, 109)
ok: (a,b,c) = (117, 44, 125)
ok: (a,b,c) = (143, 24, 145)
ok: (a,b,c) = (15, 112, 113)
ok: (a,b,c) = (105, 88, 137)
ok: (a,b,c) = (165, 52, 173)
ok: (a,b,c) = (195, 28, 197)大丈夫そうですね

コメント